|
CHAPTER XXVI.
POWER OF LOCOMOTIVES AND TRAIN RESISTANCES.
CALCULATING POWER OF LOCOMOTIVES.
THE capacity of engines is generally expressed in horse-power,
which is a measurable quantity; but, for several reasons, that
method of indicating power has not been usually applied to the
locomotive. When practical railroad men hear the size of cylinders,
the diameter of driving-wheels, and the boiler dimensions of a
locomotive, mentioned, they understand what kind of service the
engine is adapted for, and about the weight of train it can haul.
As it has been found necessary for designing and other purposes,
to estimate, with some degree of accuracy, the work a locomotive
is capable of doing, it has become usual to reckon the power of
a locomotive by the tractive force it can exert upon the rails.
PROPORTION OF ADHESION TO TRACTION.
Tractive force is the power which the pistons of the
engine are capable of exerting through the driving-wheels, to
move the engine and train. The efficiency of the engine's traction
is dependent upon the adhesion of the wheels to the rails; for,
where the adhesion is insufficient, the pistons will slip the
wheels, and no useful effect will result. To prevent the wheels
of ordinary American engines from slipping on dry rails, the weight
resting on the drivers must be about five times the power exerted
by the pistons to slip the wheels. To prevent slipping on wet,
unwashed rails, more than double the above weight would be needed.
In practice, locomotives are not provided with weight enough to
prevent the wheels from slipping on a greasy rail: the sand-boxes
provide the means of obtaining adhesion where the rails are in
bad order. A common practice is to place upon the drivers weight
equal to about six times the power exerted to slip the wheels,
which leaves a small margin for wet rails. Many locomotives have
power sufficient to slip the wheels on dry rails; but such engines
generally have boilers too small for the cylinders, or the distribution
of weight on the drivers is badly effected.
ESTIMATING TRACTIVE POWER.
The easiest way of calculating the tractive power of
a locomotive is by use of the following simple formula, first
propounded by Pambour:—
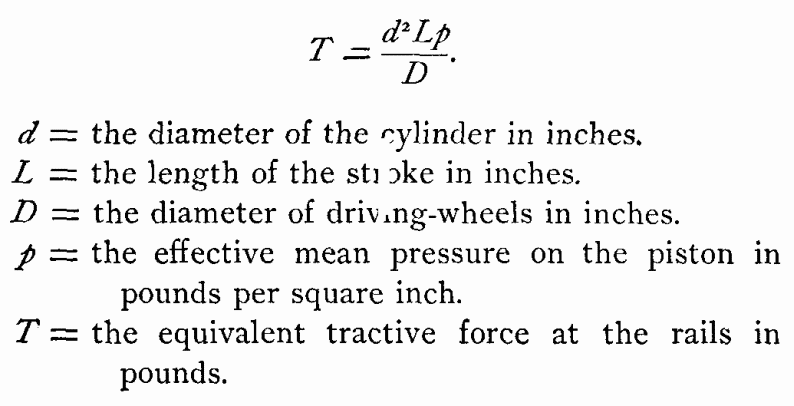
This, given in plain terms, reads: Square the diameter of piston
in inches; multiply by the length of stroke in inches; multiply
by the mean pressure of steam per square inch, and divide by the
diameter of the drivers in inches.
We will apply the calculations to the case of the standard
Buchanan passenger engine; the cylinders being 17 by 24 inches,
the drivers 68 inches in diameter, and the effective pressure
on pistons about 80 pounds. The problem is worked thus:—

This gives 8,160 pounds as the pressure exerted to turn the
drivers, which may be accepted as a close approximation to the
truth. In using this formula, the mistake has frequently been
made of taking the quotient to represent the power developed by
one cylinder, when, in fact, it gives the power of both.
A method of calculating the locomotive traction that is a good
deal followed by our engineers, is to ascertain the foot-pounds
of work the engine is doing during each revolution of the drivers.
By dividing the total thus found by the circumference of the drivers
in feet, the force exerted through each foot that the engine moves
is found. Taking the same engine, the pistons 17 inches diameter,
give 226.98 square inches area. This is multiplied by the mean
effective pressure of steam, giving 226.98 x 80 = 18158.4 pounds
pressing on each piston through the whole stroke of four feet.
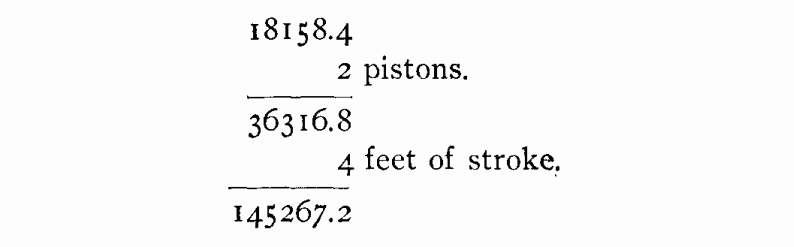
These figures show that 145267.2 foot-pounds are exerted during
each turn of the wheel, whose circumference is 17.8024; therefore,
145267 divided by 17.8024 = 8160, the number of pounds exerted
through each foot moved.
There is still another way of figuring out tractive power by
calculating the rotational force and the leverage through which
it is applied to the locomotive wheels. The pressure of steam
on the piston is productive of two strains on the crank-axle.
When the crank is on the dead center, the pressure upon the crank-pin
forces the axle against the axle-box without causing any tendency
to rotate: but, when the crank-pin is on the quarter, the full
leverage of the crank is available for rotation; the leverage
increasing gradually as the crank gets away from the center. The
mean effort upon the crank-pin during one revolution of the crank
is to the effort of the piston as .6366 is to 1
Now, to find the traction of the locomotive, we multiply the
length of our crank, which is 12 inches, by .6366, which gives
7.64 as the length of the crank receiving constant pressure from
the pistons. The aggregate steam-pressure has already been found
to be for each piston, 18158.4 pounds. This is multiplied by 7.64;
and the product is divided by the radius of the wheel, which is
34 inches, giving as a quotient 4080, being the power exerted
on one side of the engine. That, multiplied by 2, gives 8160 pounds,—the
same as was found by the other two methods.
HORSE-POWER OF LOCOMOTIVES.
When people wish to find the horse-power developed
by a locomotive, the indicator is generally employed, and the
calculations made from the diagram. Others figure out locomotive
horse-power as they do that of other engines. By this method,
the engine whose traction we have been investigating might have
the horsepower calculated as follows:—
No allowance has been made for frictional losses in any of
these calculations.
One horse-power is equivalent to the work performed in raising
33,000 pounds one foot high in one minute. One pound raised 33,000
feet high, or 330 pounds raised 100 feet high, would amount to
the same thing. One horse-power is usually spoken of as 33,000
foot-pounds; and engineers in this country always calculate work
by foot-pounds, — that is, so many pounds raised a certain
number of feet. To indicate the capacity of any prime motor, the
foot-pounds of work it is capable of raising in a given time must
be stated. Although the work is often done without any thing being
raised vertically, the power represented would be capable of raising
the equivalent weight in the stated time.
FORMULAS OF TRAIN RESISTANCES.
The work which a locomotive performs in pulling a train
is expended in overcoming the resistances due to wheel-friction,
gradients, curves, and atmospheric or wind pressure. Formulas
have been propounded for calculating all train resistances, but
they are utterly untrustworthy for American railroad trains. The
best known formula of this kind is that given by D. K. Clark in
his Railway Machinery. One calculation will show how misleading
its figures are when applied to American railroad train resistances.
Figured by the Clark formula, the total resistance per ton of
a passenger train running at a speed of fifty miles an hour on
a straight level track, is 22.6 pounds. By accurate records with
his dynagraph car, Professor P. H. Dudley found the total resistances
of an express train running at a speed of fifty-one miles an hour,
to be 11 pounds. The resistances are so much different under different
conditions, that nothing closer than a loose approximation can
be calculated of the work done by a locomotive, unless indicator
or dynamometer tests are made.
EXPERIMENTS OF TRAIN RESISTANCES ON THE
ERIE RAILWAY.
In experiments made with a freight train on the Erie
Railway in 1881, reported by Mr. F. M. Wilder to the Railway Master
Mechanics' Association, it was found that the total resistance
on a level track was from 3.25 to 4.5 pounds per ton at speeds
under twenty miles an hour. These figures will approximately represent
the resistance due to wheel and axial friction in summer; but
this resistance will be higher during cold weather, when the oil
in the axle-boxes gets frozen. Track in bad condition will also
tend to increase the wheel resistance, and improperly constructed
trucks and wheels will entail the use of more power to move the
train. Where trucks are so defective that they do not maintain
the wheels revolving in parallel planes, the flanges of some of
the wheels will rub on the rail, increasing the resistance. Wheels
out of round; those having the axle out of center, however slight;
wheels of different size on the same axle; and numerous other
car-truck disorders, —all contribute their share in making
a train pull hard.
CONDITIONS THAT INCREASE TRAIN RESISTANCES.
In a calm day the atmospheric resistance is very slight
under a speed of twenty miles an hour. To a fast train, atmospheric
resistance becomes an important obstruction. The atmosphere acts
on the train in various ways, that are hard to calculate with
any degree of accuracy,—head resistance to the locomotive,
which is presumably equal to the exposed area of the front of
the engine and cab in square feet multiplied by the air-pressure
due to the speed; then, various parts of the cars present surfaces
that the air strikes against, and increases the resistance; the
raised and projecting roofs of passenger coaches offer an ample
area for the wind to hold the train by; and every opening between
the cars permits the wind to obstruct, to some extent, each individual
car. Where wind is blowing freely in a direction to strike the
train on the side, the resistance is greatly increased; the retardation
being due to the wind pushing the car sidewise, so that the wheel-flanges
rub against the rail, and also to the wind obtaining a strong
hold on the front of each car. In the case of a freight train,
the resistance is greatly increased when the doors of cars are
left open; for every car in that condition acts like a parachute
to reduce speed. Freight trains arranged with box cars and flat
cars mixed, obtain more than a fair share of obstruction from
the atmosphere; for every box car that has a space opened in front
by a flat car, gets nearly the full pressure of the wind in its
front. It pays in coal to incur some trouble and delay in putting
box cars together. That also enables the brakemen to get along
the train more rapidly than where the cars are mixed.
In the experiments already alluded to on the Erie Railway,
it was found, in the absence of wind, that the first car of a
freight-train produced atmospheric resistance equal to a surface
of sixty-three feet, multiplied by the air-pressure due to speed;
and that each subsequent car offered a resistance of twenty per
cent of that due to the first car.
RESISTANCE OF CURVES.
Curved track increases the resistance of trains in
direct proportion to the shortness of curvature. In European railways,
the character of the curves is nearly always denominated by the
length of radius: in this country, a railroad curve is described
as of so many degrees. The degree of a curve is determined by
the angle subtended at its center by a chord of 100 feet. To those
who think of a curve by its radius, it may be well to explain
that a curve of one degree has a radius of 5,370 feet, and the
radius of any curve can be ascertained by dividing these figures
by the number of degrees.
WORK DONE BY A LOCOMOTIVE PULLING A TRAIN.
To pull a train up an ascending gradient, the locomotive
has to perform work similar to the operation of a pile-driving
engine in raising its driving-block. The train is the block raised
by the locomotive; and the lift is not vertical, but up an inclined
plane; yet the amount of work done is reckoned in precisely the
same way when the engine of a pile-driver raises a block weighing
1,000 pounds a distance of 30 feet, the work done is 1,000 x 30
= 30,000 foot-pounds: when a locomotive pulls a train weighing
1,000 tons over one mile rising 30 feet, the engine performs 30,000
foot-tons of work in that distance by raising the load alone.
The total amount of work done will also include the energy expended
in overcoming wheel-friction and other ordinary train resistances.
To find the tractive force which the engine must exert through
each foot of the mile traversed in pulling the train described,
we must divide the foot-pounds of work done, by the distance over
which the power was exerted. Thirty thousand foot-tons of work
is 60,000,000 foot-pounds. To this we will add 5 pounds additional
for every ton of the train for every foot advanced to cover wheel
and wind resistances, making 86,400,000 footpounds of work that
the engine has to perform in hauling the train-one mile. This,
divided by the number of feet in a mile, will give 16,363 pounds
as the work the locomotive must perform through each foot,—an
effort which is entirely within the capacity of many consolidation
engines.
RECORD OF FAST EXPRESS TRAIN MADE BY
PROFESSOR P. H. DUDLEY'S
DYNAGRAPH CAR.
Engineers interested in finding an approximation of
the work done in taking a fast train over a railroad, can make
a close estimate by studying out the figures given below by Professor
Dudley. The table shows the performance of an ordinary locomotive
upon a train composed of three eight-wheel and six twelve-wheel
cars weight 250 tons; working-weight of engine and tender, 126,000
pounds; cylinders of engine, 17 by 24 inches; diameter of drivers,
72 inches; weight on drivers, 48,000 pounds; blowing-pressure
on boiler, 135 pounds.
In starting the train, the locomotive would record a tension
of 11,000 to 12,000 pounds for one or two hundred feet of distance.
After hooking up, the tension would decrease to about 2,800 or
3,000 pounds; and, with this pull, the speed of 50 miles an hour
was attained in the fifth mile. As the speed increases, the resistance
of the air against the locomotive becomes greater, and more of
its own power is required to move itself. In starting a train,
the working adhesion of the steel-tired drivers on dry steel rails
is about 33 per cent of the weight upon them, and reduces as the
speed increases.
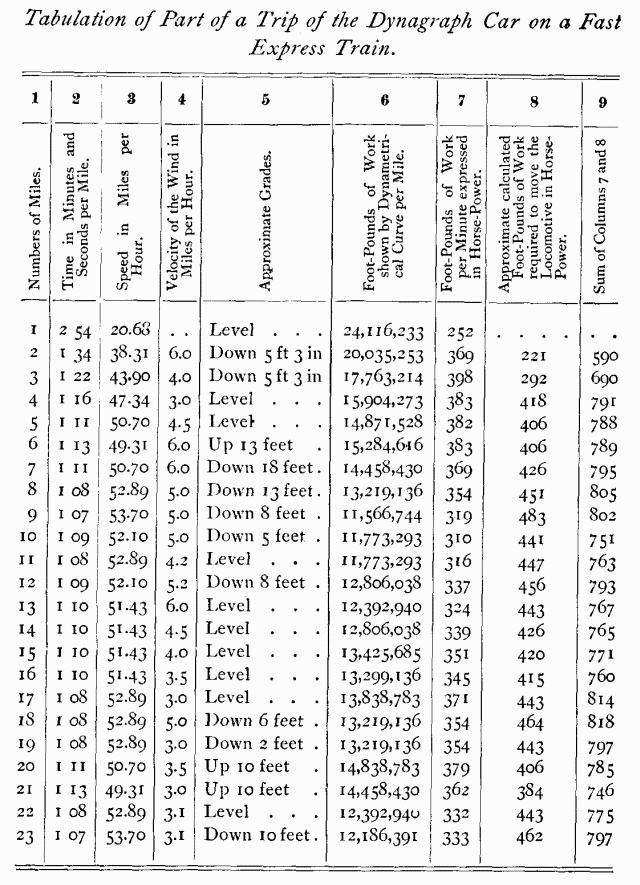
The following calculations have been made, to indicate the
trains that various locomotives ought to pull.
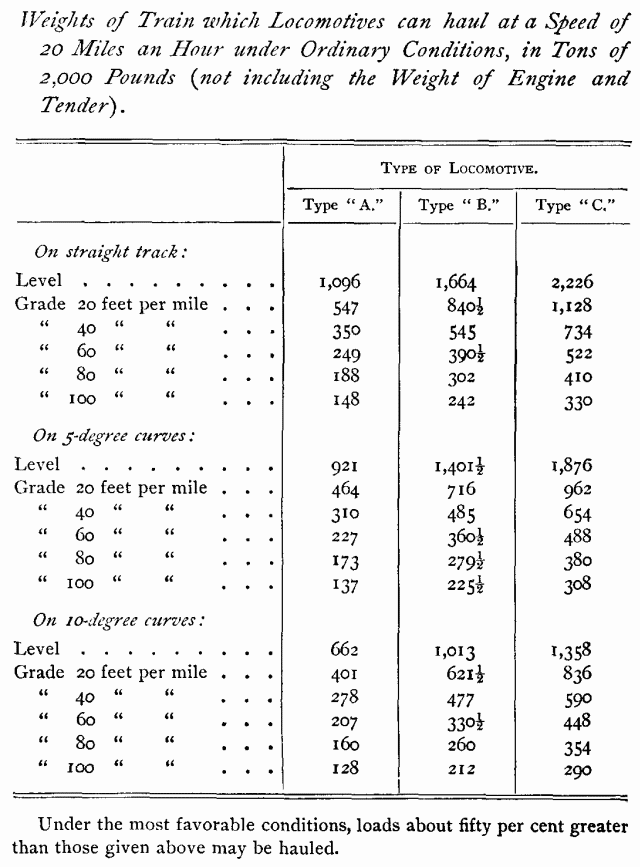
The calculations are for three types of engine, designated
in the column titles as Type "A," Type "B,"
and Type "C;" these being as follows:—
Type A. -American locomotive, with four driving-wheels,
and 12,000 pounds weight on each wheel, the total weight of engine
being 36 tons.
Type B.—Mogul or ten-wheeled locomotive, with six
driving-wheels, and 12,000 pounds weight on each wheel, the total
weight of engine being about 42 tons.
Type C. — Consolidation locomotive, with eight
driving-wheels, and 12,000 pounds weight on each wheel. the total
weight of engine being about 54 tons.
Table of Contents
| Contents Page
|







